Backtracking | The Knight’s tour problem

Backtracking is an algorithmic paradigm that tries different solutions until finds a solution that “works”. Problems which are typically solved using backtracking technique have following property in common. These problems can only be solved by trying every possible configuration and each configuration is tried only once. A Naive solution for these problems is to try all configurations and output a configuration that follows given problem constraints. Backtracking works in incremental way and is an optimization over the Naive solution where all possible configurations are generated and tried.

For example, consider the following Knight’s Tour problem.
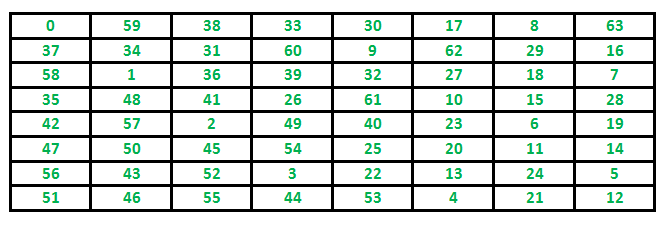
The knight is placed on the first block of an empty board and, moving according to the rules of chess, must visit each square exactly once.

Path followed by Knight to cover all the cells

Following is chessboard with 8 x 8 cells. Numbers in cells indicate move number of Knight.

Let us first discuss the Naive algorithm for this problem and then the Backtracking algorithm.

Naive Algorithm for Knight’s tour
The Naive Algorithm is to generate all tours one by one and check if the generated tour satisfies the constraints.

while there are untried tours
{ 
   generate the next tour 
   if this tour covers all squares 
   { 
      print this path;
   }
}

Backtracking works in an incremental way to attack problems. Typically, we start from an empty solution vector and one by one add items (Meaning of item varies from problem to problem. In context of Knight’s tour problem, an item is a Knight’s move). When we add an item, we check if adding the current item violates the problem constraint, if it does then we remove the item and try other alternatives. If none of the alternatives work out then we go to previous stage and remove the item added in the previous stage. If we reach the initial stage back then we say that no solution exists. If adding an item doesn’t violate constraints then we recursively add items one by one. If the solution vector becomes complete then we print the solution.

Backtracking Algorithm for Knight’s tour
Following is the Backtracking algorithm for Knight’s tour problem.

If all squares are visited 
    print the solution
Else
   a) Add one of the next moves to solution vector and recursively 
   check if this move leads to a solution. (A Knight can make maximum 
   eight moves. We choose one of the 8 moves in this step).
   b) If the move chosen in the above step doesn't lead to a solution
   then remove this move from the solution vector and try other 
   alternative moves.
   c) If none of the alternatives work then return false (Returning false 
   will remove the previously added item in recursion and if false is 
   returned by the initial call of recursion then "no solution exists" )

Following are implementations for Knight’s tour problem. It prints one of the possible solutions in 2D matrix form. Basically, the output is a 2D 8*8 matrix with numbers from 0 to 63 and these numbers show steps made by Knight.

 class Program
    {
        public static int N = 8;
        static void Main(string[] args)
        {
            solveKT();
            Console.ReadLine();
        }

        /* This function solves the Knight Tour problem
      using Backtracking.  This  function mainly
      uses solveKTUtil() to solve the problem. It
      returns false if no complete tour is possible,
      otherwise return true and prints the tour.
      Please note that there may be more than one
      solutions, this function prints one of the
      feasible solutions.  */
        private static bool solveKT()
        {
            int[,] sol = new int[8, 8];
            /* Initialization of solution matrix */
            for (int x = 0; x < N; x++)
                for (int y = 0; y < N; y++)
                    sol[x, y] = -1;

            /* xMove[] and yMove[] define next move of Knight.
          xMove[] is for next value of x coordinate
          yMove[] is for next value of y coordinate */
            int[] xMove = { 2, 1, -1, -2, -2, -1, 1, 2 };
            int[] yMove = { 1, 2, 2, 1, -1, -2, -2, -1 };

            // Since the Knight is initially at the first block
            sol[0, 0] = 0;

            /* Start from 0,0 and explore all tours using
           solveKTUtil() */

            if (!solveKTUtil(0, 0, 1, sol, xMove, yMove))
            {
                Console.WriteLine("Solution does not exist");
                return false;
            }
            else
                printSolution(sol);

            return true;

        }

        private static void printSolution(int[,] sol)
        {
            for (int x = 0; x < N; x++)
            {
                for (int y = 0; y < N; y++)
                    Console.Write(sol[x, y] + "  ");
                Console.WriteLine();
            }
        }

        private static bool solveKTUtil(int x, int y, int movei, int[,] sol, int[] xMove, int[] yMove)
        {
            int k, next_x, next_y;
            if (movei == N * N)
                return true;

            /* Try all next moves from the current coordinate
           x, y */
            for (k = 0; k < 8; k++)
            {
                next_x = x + xMove[k];
                next_y = y + yMove[k];

                if (next_x >= 0 && next_x < N && next_y >= 0 && next_y < N && sol[next_x, next_y] == -1)
                {
                    sol[next_x, next_y] = movei;
                    if (solveKTUtil(next_x, next_y, movei + 1,
                                    sol, xMove, yMove))
                        return true;
                    else
                        sol[next_x, next_y] = -1;// backtracking
                }
            }

            return false;
        }
    }